8594. Между A и B
Заданы
целые неотрицательные числа a и b (a
≤ b) и натуральное число x. Сколько существует чисел между a и b
включительно, делящихся на x?
Вход. Три числа
a, b и x (0 ≤ a ≤ b ≤ 1018, 1 ≤ x ≤ 1018).
Выход. Выведите
ответ на задачу.
|
Пример входа |
Пример выхода |
|
5 10 3 |
2 |
РЕШЕНИЕ
математика
Анализ алгоритма
Пусть f(n) равно количеству
чисел на отрезке [0; n], делящихся на x.
Пусть f(a, b) равно количеству чисел на отрезке [a; b], делящихся на x. Тогда количество искомых чисел на
отрезке [a; b] равно количеству чисел на отрезке [0; b] минус количество чисел на отрезке [0; a
– 1]. То есть
f(a, b)
= f(b) – f(a – 1)
Количество
чисел от 0 до n включительно, делящихся на x, равно n / x + 1. То есть
f(n) = n / x + 1
Если
изначально a = 0, то ответом будет
одно слагаемое f(0, b), так как
значение f(0, a – 1) не имеет смысла.
Пример
В
приведенном тесте следует вычислить значение
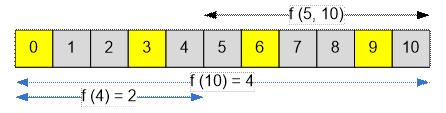
f(5, 10) =
f(10) – f(4)
Найдем
количество чисел от 0 до 10 включительно, делящихся на 3. Это будут числа 0, 3,
6 и 9. Их количество равно f(10) = 10 / 3 + 1 = 4.
Найдем
количество чисел от 0 до 4 включительно, делящихся на 3. Это будут числа 0 и 3.
Их количество равно f(4) = 4 / 3 + 1 = 2.
Следовательно
f(5, 10) =
f(10) – f(4) = 4 – 2 = 2
Реализация алгоритма
Читаем
входные данные.
scanf("%lld %lld %lld",&a,&b,&x);
Вычисляем k =
f(b), l = f(a – 1).
k = b / x + 1;
l = (a - 1) / x + 1;
При a = 0 ответом
будет значение k = f(b).
При a ≠
0 ответ равен f(a, b) = f(b) – f(a – 1) = k – l.
if (a == 0) res = k; else
res = k - l;
Выводим ответ.
printf("%lld\n",res);
Java реализация
import java.util.*;
public class Main
{
public static long a, b, x;
public static long f(long n)
{
if (n < 0) return 0;
return n / x + 1;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
a = con.nextLong();
b = con.nextLong();
x = con.nextLong();
System.out.println(f(b) - f(a-1));
con.close();
}
}
Python реализация
a, b, x = map(int,input().split())
def f(n):
if n < 0: return 0
return n // x + 1
print(f(b) - f(a - 1))